什么是大数？怎样搞出一个大数？

　　所以，加法与后继之间满足如下关系： 第三种，按倍数增加■★◆■，这就是乘法。乘法是多个加法导致的，所以乘法与加法之间满足如下关系： 第四种，一次做多次乘法■★■■◆，它通过指数来运算，它与乘法之间的关系为： 人们将后继、加法★◆■■、乘法和指数运算分别称作第0级、第1级、第2级和第3级运算★◆★。可以看到，随着运算级升高，更容易得到更大的数。

　　按上面的计数单位，俄罗斯给谷歌的罚款的数量级，在中文里读作“一百沟”，用英文里说就是“ten decillions”。

　　实际上，谷歌的创始人拉里·佩奇的确曾想将他们研发的大规模网页数据索引网站定名为googol◆◆，意喻海量的网页信息◆★。结果在注册域名时错误地输入成google，google就这样将错就错成了他们公司的名字。

　　而 ，也就是 ，它代表的运算如下，它自然就是5级运算了■◆。 你应该看出规律了吧？没错， 代表 级运算，相邻两级运算之间的关系为：

　　最简单的 ★★，它就是指数运算，即： 再看 ，它也不难◆◆■，即◆★■★： 这个指数塔，计算出来是87★◆■◆■，七万多亿■◆★★，这个数不小吧！

　　连接n维超立方体的每对几何顶点★★★★◆◆，得到一个 个顶点的完全图★■★★。将此图的每条边涂成红色或蓝色。对于n的最小值★◆■■★★，每个这样的着色至少包含一个四个共面顶点的单色完全子图是多少◆◆■★★？

　　比如说，你说a=10100很大是吧★■★★◆？那我来一个b=10100000呀◆◆◆！你嫌不够大，给出c=10b，那我就来d=10c咯，就这样下去，无穷无尽◆★★◆■，要多大就可以多大，甚至无穷大都可以。

　　第一，数必须是有根据的和来由的，不是说你想多大就多大，也就是说■◆★◆，无论多大的数，必须是有意义的◆◆。

　　看到这里，俄罗斯罚谷歌这个款的数字■■★◆，还是有点意思哦，不知是不是受到谷歌的logo中的多个o的启发？只是◆■◆，既然这个罚款如此之大■■◆★，肯定也没法执行◆★★◆■，那怎么不索性罚一个古戈尔？那样更配得上谷歌的名头了。

　　不不不★★！葛立恒数只是大数数学家族中的普通的一员，如果将大数比作恒星，那么它就像太阳一样★■，离我们最近，还有很多更大的数，比它大得多◆★。

　　如果你非要点具体的■■◆★★、刺激的感受，那你可以这样想★★◆■■■，假设全宇宙的空间都装上了墨水★★★◆◆，你用它来写3的幂塔★★★■◆■： 只要你有足够多的纸，你的寿命无限长★■■★，你就这样一直写下去★★★★■，即使用完全宇宙体积的墨水写出来的数，与葛立恒数比起来不过就是零。

　　诸君想想，基于小的数构建更大的数★★，要怎么做？废话，当然是通过运算让小的数变大啊，那么，有哪些方法呢？

　　真正的大数都不能仅靠加、乘和幂运算来获得，所以构造大数还需要考虑第二个问题——必须采用更加高级的运算法则和符号体系★◆★。

　　所以，你发现规律了，在 中，当 时■■◆，若让 增加1，则新得到的数的单箭头的数量，也就是它指数塔的层数是 ■■◆。

　　从103的“千”（thousand）开始，每隔1000升一级，直到1048的“极”（Quindecillion），计数单位的汉字（源于古印度梵书数系统[1]）和英文名称如下：

　　那么， 该有多大呢？是不是 ？不是！它是： 没错，它的连续箭头数有 个！所以★★，逆天的 甚至都无法用高德纳箭头表示了★■。

　　到现在，你大概明白了高德纳箭头的威力了■■★，就凭3个箭头，它就轻松的把这么大的数收入囊中★■■■◆。

　　iPhone 14 Pro原型机揭示了苹果Project Bongo的起源

　　如果你换个方式问◆★★■★，比如你问：像上面这样问你◆★◆■★■，问多少轮■◆★★，才可以得到一个可以表示出来地数？那么我的答案是■■■：你需要问的轮数太多了■■◆◆，这个数无法说出来。

　　我们从水平花括号的最左边开始，它是第1个3的指数塔，它有多少层呢？它的层数由第2个3的指数塔表示，这个指数塔的层数由第3个3的指数塔表示，一直这样下去◆◆★■，直到花括号上面最右边那个指数塔■★，它只有3层。这样一直进行的次数共有多少呢？这个次数又是一个指数塔，它在水平花括号的下面，它有87层★★■◆■。

　　注意看■■★★◆■，上面式子中有括号（），它告诉我们◆◆，运算是从右往左进行的。实际上，高德纳箭头的运算本身就是从右往左进行的，这种规则叫★◆★◆■■“右结合”。所以括号不是必须的■◆，但为了看清楚◆★，你也可以加上括号。

　　不过◆◆■，无论如何★■，俄罗斯的罚款还是有意义的★■■，它让2×1034这个数在现实中被实现了，而不再是虚无的数字了。

　　说明：涉及大数的计数单位，不同的文献给出的中文名称不统一，本文参考的资料给出的只是其中一种■■★◆■★，读者不必纠结具体的称谓。

　　这里面■■★，10100的名称★★“古戈尔★■■”是外来词■◆◆◆■，它是美国数学家爱德华·卡斯纳的侄子米尔顿·西罗蒂造出的计数单位“Googol◆■★★◆”的音译，它代表1后面有100个0◆★◆。它比宇宙中所有可观测的全部基本粒子数量（约1097）还多，一般被认为是最大的计数单位。

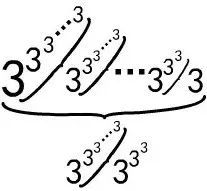
　　是的，我们已经摸到令人骇然的大数——葛立恒数的门把手了◆■★★！就是葛立恒数的最小成员，表示为 ■■■，后面依次有 一直到 ◆◆。

　　特别声明：以上内容(如有图片或视频亦包括在内)为自媒体平台“网易号■■★”用户上传并发布★★，本平台仅提供信息存储服务。

　　例如，一摩尔某单质所含的原子个数，也就是阿佛加德罗常数，它等于6.02×1023★■；IPv6协议下的IP地址总数为2的128次方，号称能使★★◆■“地球上每粒沙子都拥有一个IP地址★★■◆”；六阶魔方的状态数共有1.57153×10116种，这些数都是有意义的数。

　　i9-14900K表面被液态金属腐蚀：Intel直接拒保！无线岁半萌娃穿尿不湿参加街舞比赛 父亲回应：孩子自己模仿学会了倒立

　　很多人可能觉得这个问题有点莫名其妙，数字要多大就多大，还用得着去创造吗？

　　葛立恒数的最大数 ，是美国著名数学家■◆★◆，曾任美国数学学会主席的罗纳德·葛立恒（Ronald Graham，1935~2020）提出的[4]。它来源于一篇图论文章证明的一个数的上界，具体关联问题如下：

　　假设你每秒钟能写3个3，写完这个幂塔需要80602年■★★◆。按着键盘不动◆★★★，每秒出30个，也需要8000多年。

　　但你知道■■◆★★，这不过才刚刚开始■◆■★★，与后面的真正的大数比起来，这个数简直小到可以忽略。

　　其实◆★，葛立恒数是一个很简单的数，它的构造只需要中学数学的知识就够了。若用葛立恒数不断套娃◆◆★，例如G(65)——虽然这没有意义，得到的大数本质上还是葛立恒数的同类，实际上，仅基于指数塔和高德纳箭头构建的大数，不可能形成新的类型的大数。

　　好，继续来看 ，按照规则，它是： 是不是感觉有点炸了的感觉？没错，这个数一下子比上面所有的数大太多了，指数塔都快没法描述了，因为实在是太大了！

　　有的有的，它就是高德纳箭头■■◆★，它写作 ，这里的 是指箭头的数量，例如 就是 ■★■■◆，而 就是 ，依此类推。

　　如果你问我，葛立恒数有多大？我只能说：它大到无法回答；如果你问我，葛立恒数的位数有多大■◆◆★★？我依旧只能说：它大到无法回答；如果你继续问我★■，记录葛立恒数的位数的那个数的位数有多大？我还是只能说◆■★：它大到无法回答◆■。如果你继续问我■◆◆■◆，记录葛立恒数的位数的那个数的位数的位数有多大？我的回答依旧如此■■■◆■。

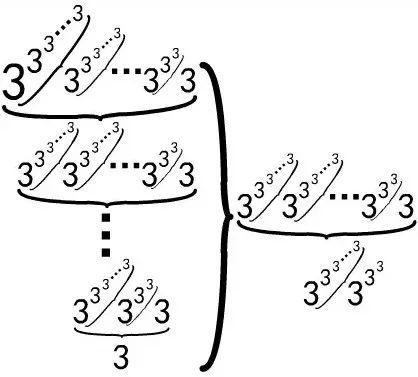
　　那么接下来的 多大？， 在它面前简直可以忽略不计，其展开图表示如下，读者可照上面的类似的方法来理解。

　　由上可见，对 来说◆★◆★， 的增长会引起数剧烈变大，例如 的指数塔的层数是 ；而如果 增加的话，那数的增加会更加快，例如 ，它的指数塔的层数的层数的层数层数 都不止 ◆■■◆◆★，简直让宇宙都丧心病狂了◆◆！

　　接下来再看 ◆■◆，你可能觉得它不过比上面那个数大一点，那你就错了！我们来看： 这个数由有多大★■？上面那个87层的指数塔的巨大数字，现在成了这个数的指数塔的层数，如下所示★■： 看到了吧，如果不借助高德纳箭头，这可不只是一个大到无法想象的数，而是一个大得无法记录的数！

　　第一种，最简单的，就是增加1★★◆★■，这叫后继。用 表示★■，例如： 第二种，一次性增加若干个1，这就是加法。它比后继运算高级，它可以替代冗长的后继运算，例如◆■★：

　　苹果性价比神机即将来袭◆◆★◆★：iPhone SE 4 相机模块被曝 12 月量产

　　并且■★■■★，以googol为基础构造的词语googology，是研究如何表示大的自然数的学科——“大数数学”的英文名称，下图中的圆形图案是大数数学的一种常见Logo。

　　比葛立恒数大的数，典型的如TREE(3)，它是目前发表在数学期刊上的最大数，它是依赖于树结构导致的一个超级无敌变态的大数，在它面前，葛立恒数可以忽略不计。

　　可以看到，葛立恒数相邻的成员中，小的与大的比起来，就像一个微粒与宇宙的相比，这是葛立恒数之所以是大数的最重要特征。

　　而更高级的大数构造方法，就需要更多高深数学知识了，比如康威链（高德纳箭头扩展）★■◆★■、ω进制线性数阵★■、树状结构和BO的结构等等[5]。本文篇幅有限，就不过多涉及了。